,
,
and
,
with
perpendicular to the disc thru its center.
|
A few days later he [Feynman] was eating in the student cafeteria when someone tossed a dinner plate into the air—a Cornell cafeteria plate with the university seal imprinted on one rim—and in the instant of its flight he experienced what he long afterward considered an epiphany. As the plate spun, it wobbled. Because of the insignia he could see that the spin and the wobble were not quite in synchrony. Yet just in that instant it seemed to him—or was it his physicist's intuition?—that the two rotations were related. He had told himself he was going to play, so he tried to work the problem out on paper. It was surprisingly complicated, but he used a Lagrangian, least-action approach and found a two-to-one ratio in the relationship of wobble and spin. That was satisfyingly neat. Still, he wanted to understand the Newtonian forces directly, just as he had when he was a sophomore taking his first theory course and he provocatively refused to use the Lagrangian approach. He showed Bethe what he had discovered. – James Gleick, Genius – The Life and Science of Richard Feynman |
The applet above animates the free rotation of a rigid body (plate, disc, ...) and examines the condition under which it wobbles as it rotates. To start the display, press the NEXT button on the bottom of the applet. A plate will appear on the display screen.
To observe what is meant by wobbling, press the START button. Notice that the red medallion on the plate is going around and at the same time the plate is wobbling. Can you say which motion (rotation or wobbling) is faster?
To visualize these motions we fix in the disc three mutually
perpendicular axis vectors
,
,
and
,
with
perpendicular to the disc thru its center.
For fuller instructions on working with the applet choose HELP... from the HELP menu. In particular this will show you how to rotate the entire display in order to see clearly what is going on.
The following three Explorations will help you learn the difference between the small wobbling and the large wobbling of the plate. You will discover a very interesting behavior of the traces of the tips of the body-fixed axes vectors.
Set the applet to show the disc by selecting DISC from the RIGID BODY menu. From the VIEW menu select BODY-FIXED AXES and TRACES to let the applet display the body-fixed axes
,
,
and
along with their traces. Make sure the LABORATORY FRAME is chosen in the REFERENCE FRAME menu.
Then set the following initial conditions for the simulation:
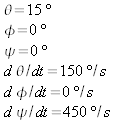
Before starting the simulation, sit back and guess what curves
the tips of the unit vectors
,
,
and
will follow. Now start the simulation. What is the curve followed by
the tip of the
vector? Is that what you predicted? What are the curves traced out by
the tips of the vectors
and
?
Are those closed curves?
HINT: To see better what is going on, you might want to drag the display area with your mouse. This allows you to change your viewing point. For the details consult HELP... in the HELP menu.
Press RESET and set different initial conditions:
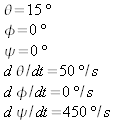
Before starting simulation, guess if the disc wobbling will be
larger or smaller this time. Start the simulation and watch the
motion of the tips of the vectors
and
.
What curves do their tips follow in this case? Are these curves
closed or open (at least approximately)?
Try other sets of initial conditions to verify your conclusions about large and small wobbling amplitudes from Explorations 1 and 2.
Set the following initial conditions:
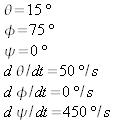
These initial conditions will lead to small amplitude of wobbling of
the disc. Press START and wait until the tips of the vectors
and
complete their circles. At that moment be ready to stop the
simulation. You will notice that the two circles intersect at two
points – one in front, and one in back. (You may have to rotate
the whole display to identify these crossing points.)
Press repeatedly the STEP BACK button until the tip of the
vector reaches the front intersection point of the red and blue
circles.
Now step the simulation forward until the tips of the
and
vectors trace out one quarter of their circles. At the same
time observe the resulting behavior of the
vector that is always perpendicular to the
and
vectors.
What fraction of its circle does the
vector trace out? Can you see why?
Now continue stepping forward until the tips of the
and
vectors trace out the second quarter of their circles. This
should leave the tip of the
vector in the back intersection point of the red and blue circles.
What fraction of its circle has the tip of the
vector traced out from the beginning?
In the light of your previous observations, what conclusion can you make about the ratio of frequencies of wobbling and rotation of the disc?
Note: Please notice that there is a direct relationship
between the
vector
and wobbling of the disc, since the
vector
is always perpendicular to the disc. Moreover there is a direct
relationship between motion of the vectors
and
on their circles and rotation of the disc.
Now
you have seen the reason of the 2 : 1 wobble to rotation
ratio. The tips of the
and
vectors are tracing out circles with the same center but lying in a
slightly different planes. This leads automatically
to the 2 : 1 ratio. But a natural question at this moment
is: Why circles? To
answer this, it is necessary to analyze the motion of the disc using
Newton’s laws. It’s a big challenge. Try doing it
yourself or consult this
document for some
hints.
The applet above uses Open Source Physics library developed by Dr. Wolfgang Christian et. al. at Davidson College. It's source code is published here under the GNU GPL licence without any guarantee. For the details, please see the text of the licence.
Java applet programmed by Boris Gazovic, Alexander Tomori, and Slavomir Tuleja, February 2004.
Explorations written by Slavomir Tuleja and Jozef Hanc, Draft version of July 2004.